今天我們要來實作基於 QSVT 的振幅放大演算法。首先我們定義：

def amplitude_amplification(
        circ: QuantumCircuit,	# `circ` 是用來準備初始態的電路 
        state: str,				# state = "011" 代表 |t> = |011>
        positions: list,		# 我們可能只想放大「部分的」量子態，因此要指定位置 (稍後舉例)
        transformation = 'chebyshev' # 指定用於 AA 的函數，此處省略不談
) -> QuantumCircuit

假設初始態 和目標態 是 qubit 的量子態；為了要在投影空間做 phase shift (QSVT 中的 )，我們需要一個輔助 qubit。於是我們宣告：

n = circ.num_qubits
qr = QuantumRegister(n + 1)
qc = QuantumCircuit(qr)

接下來，我們必須指定用來逼近 sign 函數

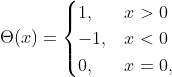
的角度序列 (其代表一個多項式)；這裡，我們使用 pyqsp 來產生角度：

pyqsp --plot-npts=4000 --plot-positive-only --plot-magnitude --plot --seqargs=21,1.0e-20 --seqname fpsearch angles --output-json

執行上述指令可以得到一 Wx-convention 的角度序列：

Wx_seq = [-1.6289766249603586, -1.454208011876622, -1.7462485302871582, -1.3357954977223736, -1.8662600481340057, -1.213725811224108, -1.9908459961512452, -1.0861701139264175, -2.1218145928902925, -0.9513642785202095, -2.260851457478332, -0.8077485591343427, -2.4093286369239166, -0.6542153401660733, -2.567999066787916, -0.49046601602792345, -2.736605610844485, -0.3174051062134276, -2.9135294062485397, -0.13739160893601188, -3.0957015611621053, -3.0957015611621053, -0.13739160893601188, -2.9135294062485397, -0.3174051062134276, -2.736605610844485, -0.49046601602792345, -2.567999066787916, -0.6542153401660733, -2.4093286369239166, -0.8077485591343427, -2.260851457478332, -0.9513642785202095, -2.1218145928902925, -1.0861701139264175, -1.9908459961512452, -1.213725811224108, -1.8662600481340057, -1.3357954977223736, -1.7462485302871582, -1.454208011876622, -1.6289766249603586]

利用之前在 QSVT 基本框架實作提到的 convert_convention(...)：

d, phi_seq = convert_convention(Wx_seq)

# phi_seq *= -2 是為了符合 Rz (以 Z 為軸的旋轉) 閘的定義: 若我們的 phase 是 p，則我們需要轉 -2p。
# 也就是說，phase 和旋轉角度之間存在 -2 這個常數倍數的差異！
phi_seq *= -2

完成這些準備工作後，剩下就是單調的 QSVT 操作啦 (詳見完整程式碼)！

等等，既然這是基於 QSVT 的 AA，為什麼我們不直接使用之前實作的基本框架呢？這是因為，在基本框架中， ；但是在這裡，，而 和 可以任意變動！不過別擔心，之後的實作應用將會使用該框架！

最後，來看看我們剛剛完成的 amplitude_amplification(...) 要如何使用！首先建立準備 的電路 ：

# 欲操作的量子暫存器大小
n = 3
# 這裡指定 positions = [0, 1]，代表整個只有前兩個 qubit 是 AA 的對象
positions = [0, 1]
# |t> = |11>
search_state = "11"

# 以下即為電路 Q
circ = QuantumCircuit(n)
circ.h([0, 1, 2])
circ.x(0)
circ.cp(theta=np.pi/3, control_qubit=0, target_qubit=1)
circ.rz(phi=np.pi/6, qubit=2)
circ.h([0, 1, 2])

# 使用上述定義的 AA
qc = amplitude_amplification(circ, search_state, positions, 'AA')

下圖為電路 Q：

	 ┌───┐   ┌───┐            ┌───┐
q_0: ┤ H ├───┤ X ├────■───────┤ H ├
     ├───┤   └───┘    │P(π/3) ├───┤
q_1: ┤ H ├────────────■───────┤ H ├
     ├───┤┌─────────┐  ┌───┐  └───┘
q_2: ┤ H ├┤ Rz(π/6) ├──┤ H ├───────
     └───┘└─────────┘  └───┘  

模擬後測量，我們可以得到：

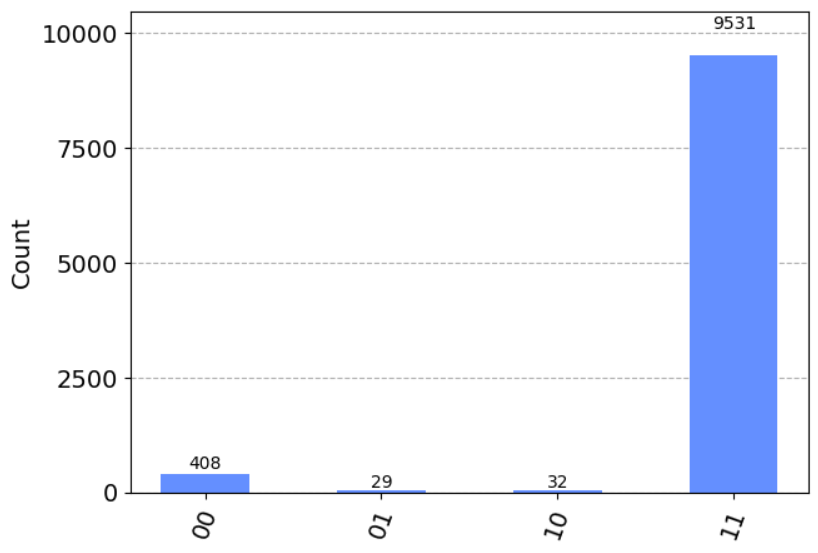
成功！